Le nombre d’or

Agrandir

Fermer

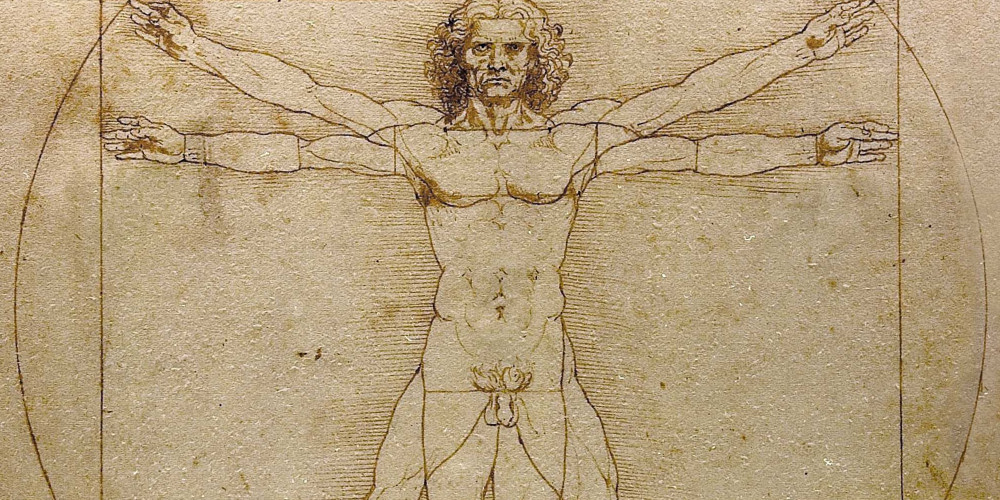
L’Homme de Vitruve

À la Renaissance, l’intérêt pour le modèle antique et la redécouverte des textes anciens vont de pair avec un courant de pensée qui place l’homme au centre du monde et en fait un modèle pour la création artistique : c’est l’humanisme.
Les humanistes restent convaincus que le monde est une création de Dieu. L’homme, également création divine, est donc parfait, et ses proportions peuvent servir d’unités de mesure. Ce qui explique que depuis l’Antiquité, on calcule les distances en pieds, en coudées ou en pouces.
Sur cette célèbre image, Étude des proportions du corps humain selon Vitruve, l’artiste Léonard de Vinci met en scène l’homme au centre de l’univers, et étudie les proportions entre les différentes parties de son corps. Par exemple, quand les bras sont tendus à l’horizontale, leur longueur équivaut à la hauteur totale du personnage : l’homme s’inscrit exactement dans un carré.

Accéder à la notice de l'image

© Gallerie dell’Academia di Venezia, Gabinetto dei disegni e delle stampe

Pour les Grecs de l’Antiquité, le monde repose sur les idées d’ordre et d’harmonie : c’est un cosmos dont tous les éléments doivent obéir à des lois physiques et mathématiques rigoureuses qui le rendent parfait. Les Grecs ne le formulent pas alors ainsi, car ils ne disposent pas encore des concepts mathématiques nécessaires, mais cette harmonie à l’œuvre dans la nature est liée au nombre d’or. À partir de la Renaissance, les savants, artistes et architectes qui étudient ce rapport parlent de "divine proportion".

À partir des polygones

Connu depuis la plus haute Antiquité mais de manière empirique, étudié par Pythagore au 6^e siècle avant J.-C., le nombre d’or ne sera théorisé par écrit que trois siècles plus tard par le mathématicien grec Euclide. Euclide étudie les polygones réguliers. Partant d’un pentagone régulier inscrit dans un cercle, il montre comment le rapport de sa diagonale (AC) à son côté (AB) correspond au nombre d’or. Ce rapport harmonique particulier s’exprime par un nombre que, par allusion au sculpteur Phidias, celui du Parthénon, on désigne plus tard par la lettre de l’alphabet grec : Ф (phi). La valeur numérique de Ф n’a pu être évaluée par une méthode mathématique et rigoureuse que grâce à la trigonométrie et l’invention de la racine carrée au 2^e siècle avant J.-C.
Il est égal à :

Agrandir

Fermer

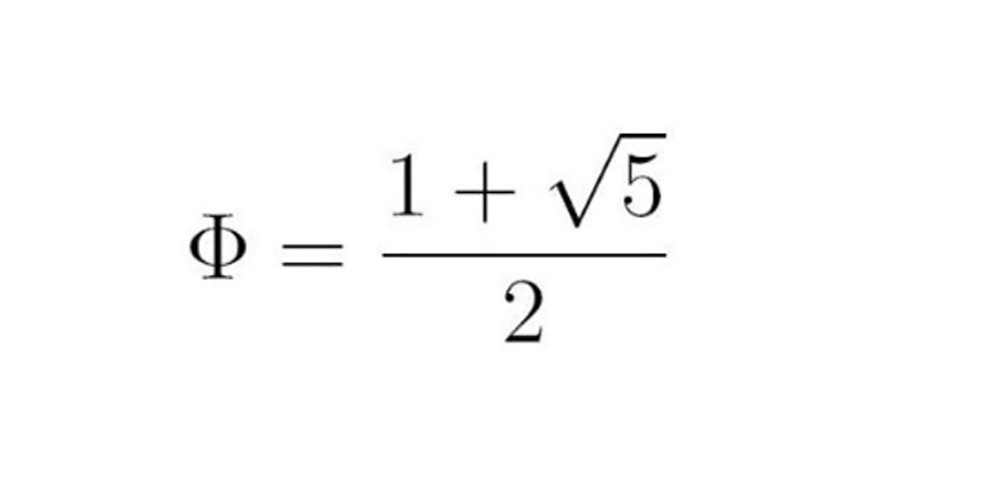
PHI

Soit environ 1, 618.

Une proportion universelle

Cette proportion se retrouve dans la nature (le cœur des marguerites ou des tournesols, la disposition des pommes de pin ou les coquilles de certains coquillages). À la Renaissance, elle est identifiée dans les proportions du corps humain, notamment dans le célèbre "Homme de Vitruve" de Léonard de Vinci. Au 20^e siècle, un architecte comme Le Corbusier l’applique à chacune de ses mesures. Ce rapport de 1 sur 1, 6 est si universel qu’on le retrouve dans nos objets les plus quotidiens : les pages des livres, les feuilles de papier A4, les écrans de TV ou d’ordinateur (du moins avant l’apparition des formats panoramiques ! ).